New Mathematical Model Helps Improve Filtration of Competing Contaminants

Every time we burn fuel, paint a car, or even produce “green” biogas, we release a cocktail of contaminants into the air. Many of these chemicals, such as siloxanes, toluene, or decane, are harmful to the environment and human health. They need to be captured before they escape into the atmosphere. Standard models deal with the capture of a single contaminant, but here’s the problem: these contaminants rarely come by themselves. They arrive together, often fighting for the same limited spots in the filters designed to trap them.

Imagine a crowded train at rush hour. Some passengers are pushy and determined (think “contaminant A”), while others are more passive (“contaminant B”). When the train (our filtration column) pulls in, who gets on board? And who gets pushed aside? That’s the question mathematicians Marc Calvo-Schwarzwälder (Universitat Politècnica de Catalunya–CRM), Tim Myers (CRM), Alba Cabrera-Codony (Universitat de Girona), and Abel Valverde (UPC) set out to answer. Their study, recently published in the first decile journal, International Journal of Heat and Mass Transfer, introduces a new mathematical model that predicts how two different contaminants behave when they compete for space on a filtering material.

Traditional models focus on a single contaminant and work well in simple cases, but things get complicated when multiple pollutants compete for the same space—one might stick more easily or even displace the other, making accurate predictions much more difficult.

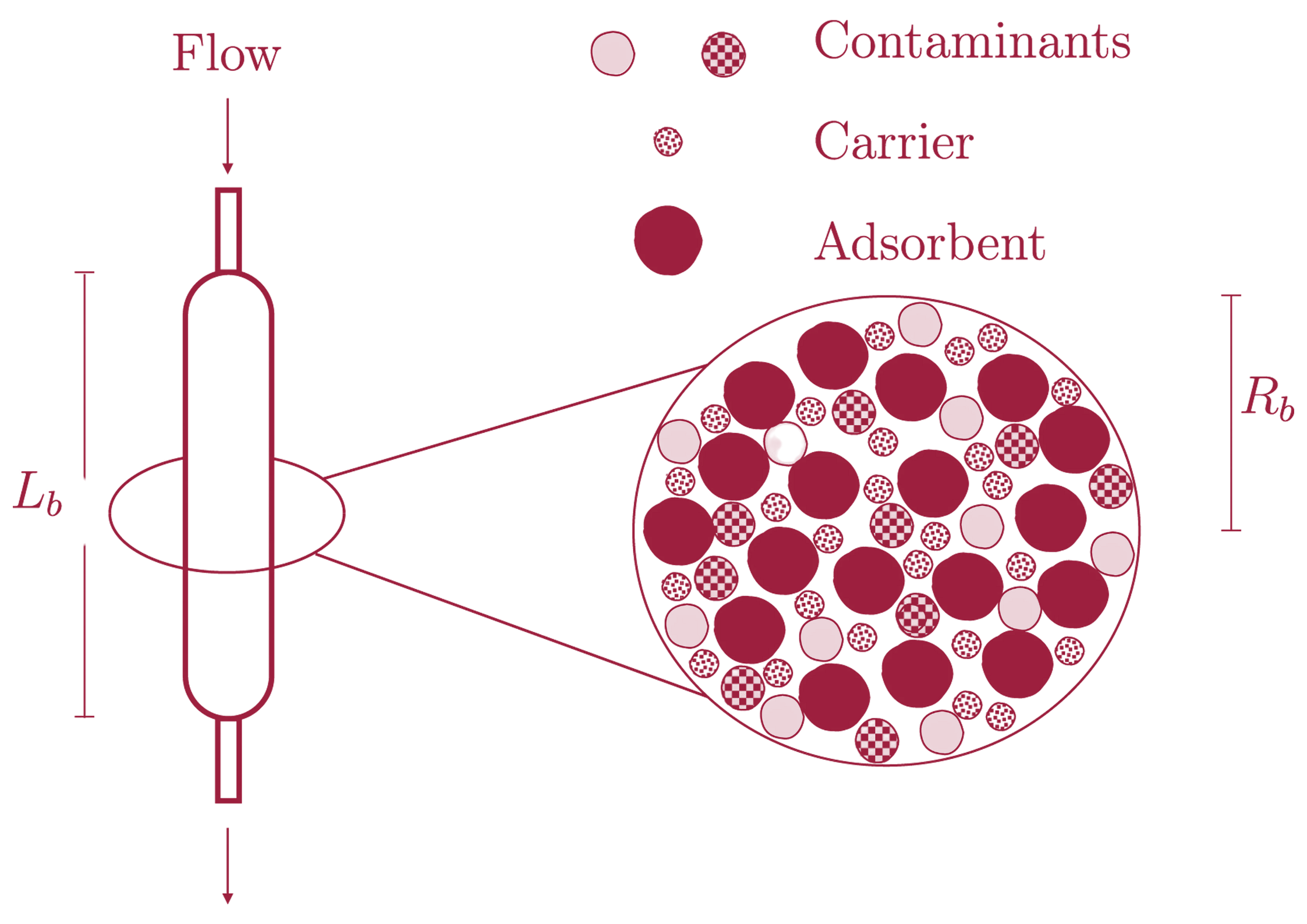
Experimental setup. A gas mixture with two contaminants flows through a column filled with an adsorbent material, the contaminants compete for the adsorption sites.

Let the Math Do the Work

To tackle this, the team developed a mathematical model that treats the filtration column like a one-way street: contaminants flow in, interact with the adsorbent and each other, and slowly advance through the column. The model captures the key physical processes involved: how the pollutants move and spread (advection and diffusion), how they stick to and detach from the filter (adsorption and desorption), and how they compete for the same spots (replacement dynamics).

One of the key tools the researchers used is the idea of a “travelling wave”. This concept, borrowed from mathematical physics, allows the team to simplify a complex system of partial differential equations into a problem involving a single variable. “After the initial stages of the process,” explains Tim Myers, “we have a contaminant wave moving between the region in the column that is full of contaminant and a region far ahead where the adsorbent material is clean. By choosing a coordinate system that travels with this wave, we can find a fixed shape.”

“Mathematically,” he continues, “this means we can reduce a system of partial differential equations to a problem involving a single variable. This is much easier to solve and permits us to make analytical progress. Effectively, we can see how all the system parameters affect the adsorption process and thus how to improve or optimise the system.”

Building on the classic single-contaminant models (developed recently by the group), they introduced a new way to track how much of the filter’s surface each pollutant occupies and how much space remains free. As the pollutants travel through the column, each tries to stick wherever it can. However, because they are competing for the same sites, a stronger contaminant can push a weaker one off the filter and take its place.

The model uses simple chemical reaction rules to describe these behaviours, combined with equations that track the pollutants’ movement. The result is a compact yet powerful representation of a very messy process. To highlight the most influential dynamics, the researchers applied a non-dimensional formulation: all the quantities were rescaled so that only the key effects were retained.

“We let the maths do the work!” says Myers. “Common sense may help in deciding what is important and what isn’t, but we prefer to use non-dimensionalisation techniques. The size of the coefficients tells us which terms matter. Neglecting the small terms, we can simplify a model and have an idea of the expected errors resulting from the approximation.”

This method not only helps simplify the model but also allows researchers to estimate how far off the approximations might be. From there, they applied techniques such as the travelling wave approximations to find analytical solutions, which are more transparent than purely numerical ones.

“With an analytical solution,” adds Myers, “we can see exactly how system parameters affect a process and consequently identify ways to make improvements.”

Real-World Testing

A good model must match reality. The team validated their predictions using experimental data with real contaminants, including siloxanes and toluene on activated carbon, achieving over 98% accuracy (R²>0.98).

“The quality of the experimental data is critical,” says Marc Calvo. “The validation of the model, and therefore the conclusions drawn, depends on it. And it’s not enough for a single experiment to verify the results. To reduce the risk of misinterpretation, it is important to compare our solutions with multiple experiments, as we did in this work.”

This strong agreement suggests the model can better guide filter design and anticipate how more complex mixtures behave. But it also relies on key simplifications—only two contaminants at a time, irreversible attachments, and dominant species behaviour. “Neglecting desorption has been a critical assumption,” acknowledges Calvo. “Numerical simulations indicate that if this mechanism is included, the travelling wave strategy is no longer valid.”

“We have recently been able to solve the problem in the reversible case as well,” he notes. “But when more than two contaminants are considered, the modelling part becomes significantly more complex, and the number of assumptions increases. It will be crucial to have experiments that help us understand the processes and incorporate them into the model.”

And if you’re still wondering whether math can make a difference, Myers shares this anecdote: “A group of engineers once clapped when I finished demonstrating how a simple mathematical model could predict the ice growth on an aircraft. When I asked why they clapped, I was told no one thought a mathematician could solve their problem.”

Citation:

Calvo-Schwarzwälder, M., Cabrera-Codony, A., Valverde, A., Myers, T.G. (2025). An analytical model for column adsorption with two competing contaminants. International Journal of Heat and Mass Transfer, 245, 124938. https://doi.org/10.1016/j.ijheatmasstransfer.2024.124938