De la COVID a la concurrència: Joachim Kock (CRM-UAB) resol un vell problema obert en informàtica teòrica

A l’inici de la pandèmia, en Joachim Kock (CRM-UAB) va començar a experimentar amb models epidemiològics. Inesperadament va fer un descobriment matemàtic que el va portar a solucionar un problema d’informàtica teòrica obert des dels anys vuitanta. El seu article amb el resultat acaba de ser publicat a la prestigiosa revista d’informàtica Journal of the ACM (Association for Computing Machinery).

La COVID i les xarxes de Petri

Un dels models matemàtics més simples i més utilitzats per a descriure epidèmies és el model SIR. Aquest model divideix la població en tres grups (o compartiments): les persones sanes (S), les persones infectades (I) i les persones recuperades i per tant immunes (R). El model estipula que hi ha dues transicions possibles entre els compartiments: la primera té lloc quan una persona sana es troba amb una d’infectada, i el resultat és que totes dues esdevenen infectades. L’altra transició té lloc quan una persona infectada es recupera.

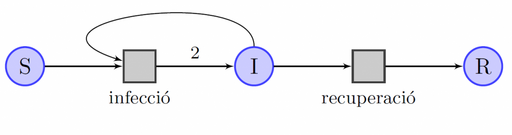
Les relacions entre els compartiments i les transicions es poden visualitzar amb la figura següent, que és un exemple d’una xarxa de Petri:

Els cercles representen els compartiments, els quadrats representen les transicions possibles i les fletxes enllacen els compartiments que participen en les transicions. El fet que dues persones resultin infectades en la primera transició s’indica a la xarxa de Petri amb el pes 2 a la fletxa corresponent.

Per utilitzar la xarxa de Petri i predir l’evolució de contagis i recuperacions en una situació real, són necessaris dos paràmetres que indiquen amb quina taxa s’efectuen les transicions i també cal conèixer la distribució inicial de persones. De l’estimació d’aquests paràmetres se n’encarreguen investigadors dels camps de la medicina i de l’estadística. Llavors, a partir de la xarxa i dels paràmetres, s’escriuen unes equacions diferencials les solucions de les quals descriuen l’evolució dels elements de cada compartiment.

Les xarxes de Petri tenen el seu origen en la química. Van ser inventades per Carl Adam Petri el 1939 quan tenia només 13 anys. Originalment, els compartiments eren concentracions de substàncies químiques en una solució i les transicions eren reaccions químiques. Mica en mica les xarxes de Petri van anar trobant usos en altres camps de modelització d’evolucions, com ara l’evolució de poblacions d’animals en circuits ecològics. Quan s’utilitza el model SIR en epidemiologia, en realitat els compartiments S, I, i R s’interpreten com a concentracions, i el model descriu com evolucionen.

A l’inici de la pandèmia, quan J. Kock va començar a experimentar amb modelització de la COVID-19, volia tractar a les persones del model com a individus, enlloc de com a concentracions. Aquesta idea la va tenir a arrel dels seus coneixements en informàtica teòrica.

Computació concurrent i el problema de semàntiques

En informàtica teòrica les xarxes de Petri s’utilitzen d’una manera diferent, no amb paràmetres continus i equacions diferencials sinó amb eines de matemàtica discreta. Els compartiments i les transicions ja no simbolitzen concentracions i reaccions. En comptes d’això, els compartiments tenen un nombre petit de fitxes (tokens) que es mouen d’acord amb les transicions. Una transició pot disparar-se si hi ha fitxes suficients als compartiments d’entrada. Llavors aquestes fitxes es consumeixen i produeixen fitxes noves als compartiments de sortida.

Un dels usos principals de les xarxes de Petri en informàtica és com a model de computació concurrent, és a dir, descriure processos computacionals que concorren amb alguns recursos compartits (les fitxes). La teoria de la concurrència en aquest sentit tècnic també és molt important en l’estudi de cadenes de producció, distribució, logística o business modelling, entre d’altres. Hi ha molts aspectes de la computació concurrent que es poden descriure amb l’ajut de les xarxes de Petri i permeten estudiar, per exemple, si una xarxa pot funcionar indefinidament o si en algun moment haurà de parar per falta de recursos. Aquí pot continuar l’analogia amb les xarxes químiques: un procés químic, com ara una combustió, s’atura si li falta oxigen. O en el cas d’una pandèmia, s’acaba quan no hi ha més contaminats.

Per entendre el problema d’informàtica que ha resolt J. Kock cal introduir una mica de terminologia. Un estat d’una xarxa de Petri és una distribució determinada de fitxes als compartiments. Un procés d’una xarxa és essencialment passar d’un estat a un altre mitjançant disparaments de transicions. Bàsicament hi ha dues maneres de formalitzar tots aquests conceptes matemàticament amb el que s’anomena la semàntica operativa de les xarxes de Petri.

Les dues maneres són importants per a l’anàlisi de la computació concurrent ja que donen informació complementària. La primera consisteix en dir que un procés és una seqüència de disparaments. Això defineix un sistema algebraic a on es poden encadenar seqüències (si l’estat final d’una coincideix amb l’estat inicial de l’altre) per a formar seqüències més llargues. L’altra manera consisteix en considerar només la relació de causalitat en una configuració de disparaments, però sense que segueixin una seqüència necessàriament. Aquest últim és un enfocament geomètric, perquè la configuració de disparaments és formalment una funció d’un graf cap a la xarxa.

L’enfocament algebraic té avantatges per a realitzar càlculs, però no explica bé els aspectes de concurrència i de causalitat. En canvi l’enfocament geomètric explica amb claredat aquests termes però té el problema que no permet encadenar dos processos per a obtenir-ne un de més llarg ja que no hi ha una manera única d’enganxar dos grafs. Les dues semàntiques coexisteixen, però des dels anys vuitanta hi havia el problema obert de reconciliar-les. És un problema en el qual hi ha treballat molta gent, però a arrel d’uns articles publicats al voltant de l’any 2000 es considerava que el problema no podia tenir solució.

Un nou plantejament: aspectes categòrics i homotòpics

La idea de J. Kock va ser la de traçar a les persones individualment en les simulacions de la COVID-19, de manera semblant a l’ús de les xarxes de Petri en informàtica. “En retrospectiva, no va ser una bona idea des del punt de vista de l’epidemiologia”, diu J. Kock. Utilitzar models discrets no porta problemes però tampoc té avantatges respecte els models continus. Fent provatures, però, va descobrir que era impossible traçar les persones individualment, no pels grans nombres de la població si no perquè el formalisme de les xarxes de Petri no ho permet. Va trobar un obstrucció principal per a rastrejar fitxes individualitzades en una xarxa de Petri convencional i va resultar ser la mateixa obstrucció que impedia la reconciliació de les semàntiques algebraica i geomètrica.

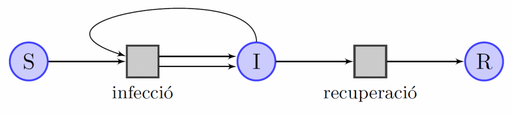
J. Kock llavors es va embarcar en una revisió completa de la teoria de les xarxes de Petri: “Calia modificar la pròpia definició de xarxa de Petri, i la modificació té a veure amb els meus camps d’especialització, la teoria d’homotopia, la teoria de categories i la combinatòria. La modificació és molt lleugera, i pot semblar sorprenent que tingui un efecte tan gran: consisteix simplement en utilitzar fletxes paral·leles en comptes de pesos, és a dir, passar d’un nombre natural a un conjunt (de fletxes) amb aquest nombre d’elements. En teoria d’homotopia, aquest tipus de consideració és habitual.” El que faltava a les xarxes de Petri convencionals era l’accés a la informació de les simetries d’una xarxa.

Impacte multidisciplinari

La reconciliació de les dues semàntiques és important per a la teoria de les xarxes de Petri però no té gaire efecte en les aplicacions. De fet, és una característica important que la modificació de la definició per a gairebé totes les aplicacions sigui retrocompatible. Es poden seguir fent servir les xarxes de Petri com en els últims 30 anys.

Tot i així, el nou enfocament i la nova definició han portat a avantatges en els càlculs de les aplicacions. I, curiosament, aquests avantatges han acabat repercutint en el camp de l’epidemiologia. Patterson i els seus col·laboradors recentment han desenvolupat un mòdul de xarxes de Petri per al llenguatge de programació científica ‘Julia‘ fent servir la nova definició. El fet que aquesta definició sigui purament combinatòria (mentre que la tradicional amb els pesos és una descripció híbrida combinatòria-algebraica) ha facilitat la implementació i la interacció amb altres mòduls de Julia. Aquesta nova teoria l’han aplicat en la modelització de la COVID-19, per tant la recerca de J. Kock ha acabat tenint impacte també en línia amb la seva intenció original.

Aquest treball és un exemple de recerca interdisciplinari en varis aspectes. Fent proves per millorar els models epidemiològics, J. Kock ha acabat contribuint a la informàtica teòrica. Per altra banda, ha necessitat eines de camps diferents d’aquest per poder resoldre el problema, tals com la teoria de categories i la teoria d’homotopia. També li ha calgut tenir coneixements suficientment amplis per a poder imaginar noves interaccions entre els camps i identificar les eines adients. Finalment, ha acabat millorant models epidemiològics indirectament a través dels mòduls del llenguatge de programació Julia.

“Crec que hi ha vàries morals en aquesta història”, reflexiona J. Kock. “La primera, que les matemàtiques abstractes permeten transferir coneixements i experiència d’una ciència a una altra, a vegades de manera inesperada. Segona, que a vegades es busca una cosa i se n’acaba trobant una altra, per tant, pot ser productiu experimentar amb idees sense saber exactament a on porten.”

Referències:

Joachim Kock: Whole-grain Petri nets and processes, Journal of the ACM, vol. 70 (1), pp.1-58 (February 2023). DOI: https://doi.org/10.1145/3559103.

Desenvolupat de: https://www.uab.cat/web/sala-de-premsa/detall-noticia/resolen-inesperadament-un-vell-problema-de-la-teoria-de-computacio-a-partir-de-l-estudi-de-la-covid-1345829508832.html?detid=1345879245356

Altres enllaços:

Simuladors del model SIR: simulador 1 d’AiroDoctor, simulador 2 de GeoGebra.

Simulador de xarxes de Petri: https://apo.adrian-jagusch.de/#!/Sample%20Net