Could the Sun–Jupiter–Saturn System Truly Exist? A Computer-Assisted Approach Sheds New Light on Celestial Stability

When we picture the Solar System, most of us still see that neat little diagram from our school days with the planets lined up like obedient dancers, each tracing a perfect circle around the Sun. But the reality is far messier. Over long timescales, planetary motion is chaotic and notoriously difficult to predict. Understanding the gravitational dance between just three celestial bodies (say, the Sun, Jupiter, and Saturn) has been one of mathematics’ most enduring challenges since the time of Isaac Newton.

Now, a recent study by Jordi-Lluís Figueras (Uppsala University) and Alex Haro (Universitat de Barcelona and the Centre de Recerca Matemàtica) sheds new light on this centuries-old puzzle. Using a sophisticated mathematical framework known as KAM theory (after Kolmogorov, Arnold, and Moser), they’ve shown that stable, quasiperiodic motion might be possible in a simplified version of the Sun–Jupiter–Saturn system. Their computations, carried out with ultra-high precision, have produced convincing numerical evidence that supports the applicability of a KAM theorem to this celestial configuration.

“What our work shows,” explains Alex Haro, “is that the most astronomically significant part of the Solar System could, in fact, be stable. That’s precisely the problem Newton raised in his Principia when asking about the mutual gravitational effects between Jupiter and Saturn.”

Three Bodies, Chaos, and a Historic Puzzle

In the 17th century, Newton solved the two-body problem: a planet orbits the Sun in an ellipse. But if we introduce a third body (another planet, for instance), the problem becomes wildly more complex. This infamous three-body problem is chaotic, meaning small variations in initial conditions can lead to drastically different long-term behaviour, and no general solution exists.

In the 20th century, KAM theory offered hope. It showed that under specific conditions, stable, quasiperiodic orbits could persist even in systems susceptible to chaos; trajectories that never exactly repeat but remain bounded and regular. However, those conditions were thought to be nearly impossible to meet in real astronomical systems.

Figueras and Haro’s work challenges that view. Their study, published in the Journal of Nonlinear Science, takes real values for the masses and orbital parameters of Jupiter and Saturn and shows that even outside the narrow scope of classical perturbative methods, stable motion can still emerge. They achieved this using a refined numerical approach rooted in the parameterisation method, which allowed them to compute and validate the existence of what are known as invariant tori (geometrical objects that represent quasiperiodic orbits in phase space).

“In particular,” says Haro, “our result confirms that, in a reduced and simplified Newtonian model of the Solar System, where only the Sun and its two largest planets move on a plane, perpetually bounded, regular motion can exist, and that such motion corresponds to realistic data.”

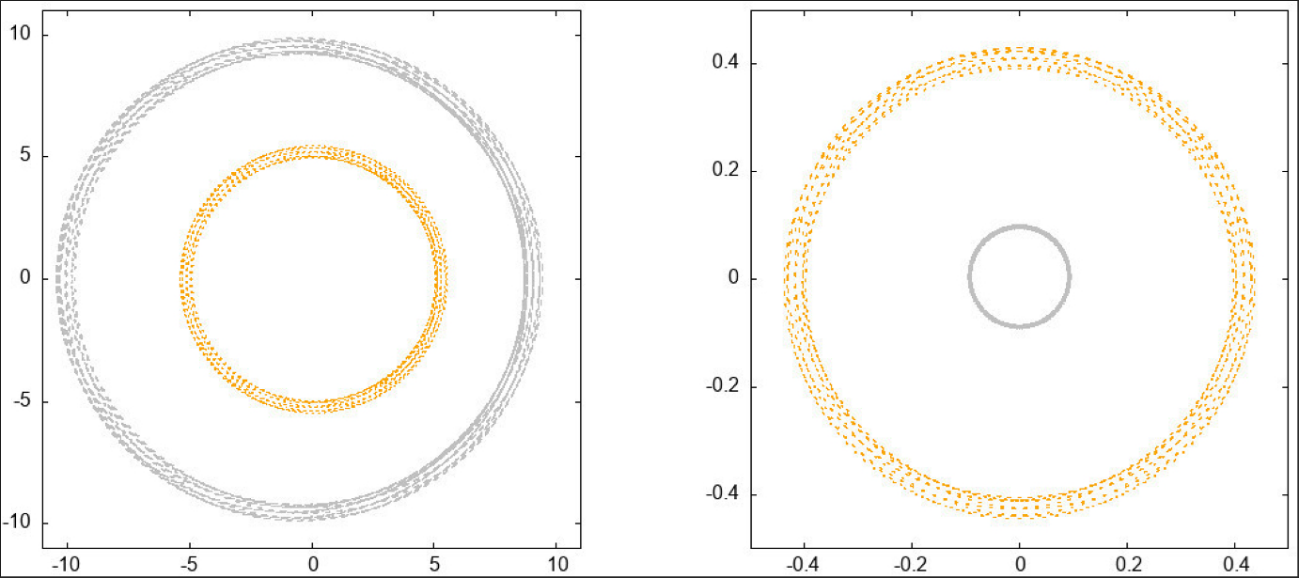
Projections of the 3d invariant torus (which generates a 4d torus) in Cartesian coordinates, showing the positions and momenta of Jupiter and Saturn. The coordinates for Jupiter are shown in orange, and those for Saturn in grey.

One of the conceptual sparks behind this work is a lesser-known observation by French mathematician Michel Hénon. Hénon suggested that some stable orbits could survive even under strong perturbations, an idea that at the time was seen as too optimistic. But Figueras and Haro took it seriously.

“Computers made these calculations possible,” says Haro, “but we couldn’t have done them without the right algorithms. These involve both the dynamical and geometric aspects of the functional equations we need to solve. And by proving the convergence of our algorithms via KAM methods, we ensure the reliability of our results.”

Among their tools is the notion of translated tori, which act as a kind of workaround for the degeneracies that normally prevent the application of KAM theory to realistic planetary systems. Their calculations, carried out with ultra-high precision on supercomputers, achieved an error of invariance as low as 10⁻⁵⁴, far surpassing the threshold required by the theory.

Although their model is limited, since it assumes planar motion and includes only two planets, the implications are far-reaching. “The final step,” Haro explains, “will be a mathematical proof of the existence of this quasiperiodic motion, with the actual frequencies of Jupiter and Saturn. This proof will be computer-assisted. The object we’re validating, a three-dimensional torus in a six-dimensional space, is encoded with over six billion Fourier coefficients.”

This step builds directly on their earlier paper, presenting a tailored KAM theorem and an iterative lemma. The third and final phase, currently in progress, will combine all these ingredients to produce a complete, rigorous, computer-assisted proof. But what happens when the methodology is applied beyond our Solar System?

“Applying this to exoplanetary systems is something we’d love to explore,” Haro says. “A key challenge is the difficulty of obtaining precise data. But our theorems are coordinate-independent, so they can be adapted to other configurations.”

The Beauty of the Problem

Haro’s interest in celestial mechanics traces back to the deep, almost mythic allure of the three-body problem. “It’s a paradigmatic problem,” he says, “one that contains both order and chaos. That makes it a testing ground for methods and ideas that often go on to apply elsewhere—even when the original problem isn’t fully solved.”

Indeed, the very foundations of dynamical systems theory were laid by Henri Poincaré while trying to understand the three-body problem. Later, KAM theory emerged from attempts to resolve the same questions. Haro points to key contributions by mathematicians like Michel Herman, Jacques Féjoz, Luigi Chierchia, and Gabriella Pinzari, as well as Vladimir Arnold’s influential mechanisms for explaining chaos and diffusion.

Haro and Figueras’ work stands on the shoulders of this tradition but carves out its own space. They’ve also collaborated with researchers like Miquel Barcelona, Renato Calleja, Chiara Caracciolo, Álvaro Fernández-Mora, Josep Maria Mondelo, and Pedro Porras on related applications, from space mission design to plasma physics. “What drew us to this problem,” Haro says, “was partly its beauty, but also the fact that many in the scientific community, especially among physicists, believed KAM theory couldn’t be applied to realistic planetary systems. That’s something Henry Dumas discusses in The KAM Story.”

“Mathematicians like challenges,” Haro says, “and this one is formidable (at least for us) because it involves difficulties at many levels, both mathematical and computational.”

“Jordi-Lluís and I had already worked on computer-assisted proofs in a different context, building on work I had previously done with Rafael de la Llave,” he adds. “Later, together with Alejandro Luque, we turned our attention to KAM theory, drawing inspiration from a key paper by Alejandra González, Rafael de la Llave, Jordi Villanueva, and Àngel Jorba. That’s when we developed our first method for computer-assisted KAM proofs, which we initially tested on simpler problems.”

Much of Haro’s journey through these ideas has been shaped by a longstanding collaboration with mathematician Rafael de la Llave. “My collaboration with Rafa has been foundational,” he says. “During my postdoc in Austin, he introduced me to a new way of doing mathematics. We developed a shared language that shaped the work I’ve done ever since.”

Together, they explored invariant tori, their associated structures, and eventually, the frontier of KAM theory for degenerate systems, work that continues to echo through Haro’s current research in astrodynamics. “We still have unfinished projects that go back to those early days,” he adds. “My connection with Rafa goes far beyond mathematics.”

While scientists like Jacques Laskar have shown that chaos leaves its imprint on the inner planets over long timescales, Figueras and Haro’s work reveals another side of the cosmic story: that even amid instability, mathematical order can survive. “Humanity has been fascinated by celestial motion since the dawn of time,” Haro reflects. “And we’re no exception.”

The Sun-Jupiter-Saturn system may be just one sliver of the sky, captured in a model. But it reminds us that beneath the turbulence of the cosmos, there is a hidden rhythm; complex, delicate, and, with the right tools, knowable.

Citation:

Figueras, J.-L., & Haro, A. (2024). Sun-Jupiter-Saturn System May Exist: A Verified Computation of Quasiperiodic Solutions for the Planar Three-Body Problem. Journal of Nonlinear Science, 34(4), Article 10109. https://doi.org/10.1007/s00332-024-10109-4