The Modern Trends in Fourier Analysis conference, held this June at the Centre de Recerca Matemàtica (CRM), gathered over a hundred researchers from around the world to explore advances in harmonic analysis. Among the invited speakers was Hong Wang, associate professor at NYU’s Courant Institute of Mathematical Sciences, who presented a lecture outlining a new geometric approach to the longstanding Stein restriction conjecture. Her talk followed closely on the heels of a landmark achievement: Wang’s recent resolution, with Joshua Zahl, of the celebrated three-dimensional Kakeya conjecture, one of the most challenging open problems in the field.
In her talk, Wang presented joint work with mathematician Shukun Wu, focused on a novel geometric method to approach the restriction problem. At its core is a deceptively simple conjecture: if a function has its Fourier transform supported on the unit sphere in ![]() , then its
, then its ![]() -norm should be controlled by the
-norm should be controlled by the ![]() -norm of its Fourier transform, for
-norm of its Fourier transform, for ![]() . This conjecture has guided decades of research in Fourier analysis.
. This conjecture has guided decades of research in Fourier analysis.
Rather than attacking it directly, Wang and Wu propose to study it through a geometric lens: they formulate a conjecture about how many times thin tubes in space can intersect. “It’s a purely geometric question about incidences,” Wang explained. “And if the conjecture holds, it implies Stein’s.” They prove the two-dimensional case and obtain new restriction estimates in three dimensions for ![]() , which in turn lead to a known bound in the Kakeya problem known as Wolff’s hairbrush estimate.
, which in turn lead to a known bound in the Kakeya problem known as Wolff’s hairbrush estimate.
Solving Kakeya in 3D
This link between restriction and Kakeya is not incidental. Wang is one of the two authors, alongside Joshua Zahl (University of British Columbia), behind the 2025 proof of the three-dimensional Kakeya conjecture, a milestone that had eluded mathematicians for over fifty years.
The conjecture, inspired by a question posed by Japanese mathematician Sōichi Kakeya in 1917, asks whether a needle (or line segment) that turns in every direction can sweep out an arbitrarily small volume. Wang and Zahl proved that in three-dimensional space, any such Kakeya set must have Hausdorff and Minkowski dimension exactly 3. That is: it may be thin, but it cannot be small.
Their proof follows a layered strategy: first solving the problem for a specific class of objects called “sticky sets,” then extending the result to more general cases. A key insight came from a concept that transformed Wang’s approach: “You can find fractal structure in any set if you look at the right scales,” she explained. This idea, originally developed by Katz and Zahl, helped her rethink how to extract order from apparent geometric chaos.
More than just technique
Wang’s interest in the restriction problem began over a decade ago. “I got interested in Stein’s restriction conjecture when I read a paper by Luis Vega (BCAM), actually ,” she recalled. That early exposure laid the foundation for her current line of research, which combines deep harmonic analysis with geometric insight.
“It’s a long journey,” she said. “Sometimes you work for years and don’t solve the problem. But the tools, the intuition, what you build along the way, it all ends up useful.” She also spoke of the difficulty of knowing when to persevere or walk away: “You have to be honest with yourself. Not too optimistic, not too pessimistic. That process, I think, is very rewarding.”
Her work is deeply tied to real geometry, not just in theory but in essence: “If you move the problem to complex space, the statement becomes false. You need tools that really distinguish real from complex. Many standard techniques don’t.”
Conferences, community, and collaboration
Beyond the mathematics itself, Wang highlighted the value of gatherings like the CRM conference. “You get a sense of what’s happening in the field, have spontaneous conversations, meet potential collaborators; that’s a fundamental part of doing mathematics,” she said.
With her recent contributions, Wang has made a significant impact on harmonic analysis and geometric measure theory. Her work combines technical depth with a clear geometric intuition, offering new tools and perspectives for longstanding problems. As Nets Katz remarked, the solution to the Kakeya conjecture marks a once-in-a-century achievement, one in which Wang has played a central role.
You can watch the full interview on the CRM YouTube channel.
|
|
CRM CommPau Varela
|
Els estudiants participants a la prova de preselecció de Bojos per les Matemàtiques visiten el CRM
La prova de preselecció de Bojos per les Matemàtiques va reunir estudiants de tot Catalunya a la UAB i al CRM, amb presentacions a càrrec de Montse Alsina, presidenta de la Societat Catalana de Matemàtiques, Núria Fagella, degana de la Facultat de Matemàtiques i...
Jordi Mompart highlights the role of artificial intelligence in sport at the XIII GEFENOL-DIFENSC Summer School
The XIII GEFENOL-DIFENSC Summer School gathered over thirty researchers from across Europe to explore how statistical physics helps explain complex phenomena in biology, ecology, networks, and social systems. In his closing lecture, Jordi Mompart (UAB) examined how...
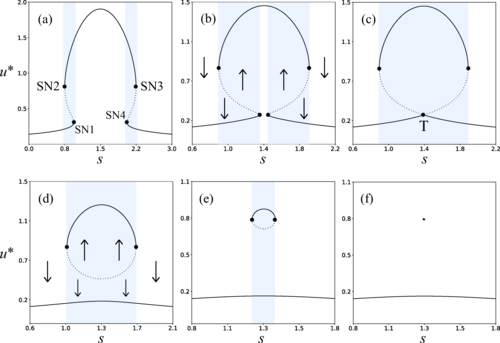
Critical Slowing Down in Genetic Systems: The Impact of Bifurcation Proximity and Noise
An international collaboration including researchers from the Centre de Recerca Matemàtica (CRM) has shown that when several bifurcations occur close to one another, their interaction can dramatically amplify critical slowing down effect - the progressive slowdown of...
Two CRM researchers begin their Marie Skłodowska-Curie fellowships
Gustavo Ferreira and Tássio Naia, CRM postdoctoral researchers and new Marie Skłodowska-Curie fellows. Gustavo Ferreira and Tássio Naia, who joined the CRM in 2023 through the María de Maeztu programme, have started their Marie Skłodowska-Curie postdoctoral...
Matroid Week at CRM: A Collaborative Dive into Combinatorial Geometries
From October 13 to 17, 2025, the CRM hosted Matroid Week, a research school on combinatorial geometries and matroid theory. Courses by Laura Anderson and Geoff Whittle explored intersection properties and structural emergence in matroids. The event fostered deep...
László Lovász receives the 2025 Erasmus Medal in Barcelona
Mathematician László Lovász received the 2025 Erasmus Medal from the Academia Europaea yesterday at the PRBB in Barcelona, where he delivered the lecture “The Beauty of Mathematics”. Renowned for his work in graph theory and discrete mathematics, Lovász has shaped...
Combinatorial Geometry Takes Shape at the CRM
For one week in early October, the Centre de Recerca Matemàtica became a meeting ground for the world of combinatorial geometry. The Polytope Week research school gathered more than fifty participants from three continents to study the interplay...
Learning the Language of Complexity: XIII GEFENOL Summer School Highlights
From October 6–10, 2025, the Centre de Recerca Matemàtica hosted the XIII GEFENOL-DIFENSC Summer School, bringing together young researchers and leading experts to explore the role of statistical physics in understanding complex systems. The program featured courses...
A Week Inside Complexity: The First CS3 Summer School at the CRM
The first CS³ Summer School on Complex Systems transformed the Centre de Recerca Matemàtica into a crossroads of ideas, where physicists, biologists, economists, and mathematicians explored how order and chaos intertwine across nature and society....
Jezabel Curbelo receives the 2025 National Research Award for Young Researchers in Mathematics and ICT
Full professor at the Universitat Politècnica de Catalunya and researcher at the Centre de Recerca Matemàtica, Jezabel Curbelo has been honored with the 2025 National Research Award for Young Researchers in the María Andresa Casamayor category (Mathematics and ICT)....
Tim Myers represents ECMI at the ICIAM Board Meeting and promotes industrial mathematics in Vietnam
ICIAM Board and VIASM Members during a breakVietnam hosted the ICIAM Board Meeting and Workshop this September at the Vietnam Institute for Advanced Study in Mathematics (VIASM), gathering 70 delegates from five continents. CRM researcher Tim Myers attended as the...
Why Your Brain Is Never Still: Representational Drift and Statistical Learning
A paper recently published in Current Opinion in Neurobiology by Jens-Bastian Eppler, Matthias Kaschube, and Simon Rumpel shows that...