Wigglyhedra: A New Combinatorial and Geometric Structure

In the article “Wigglyhedra”, researchers Asilata Bapat (Australian National University) and Vincent Pilaud (Universitat de Barcelona – Centre de Recerca Matemàtica) introduce the wiggly complex, a novel combinatorial and geometric structure, along with its associated polytope, the wigglyhedron, which bridges geometry, combinatorics, and category theory in innovative ways.

In their recent article, Wigglyhedra, published in Mathematische Zeitschrift, Asilata Bapat (The Australian National University) and Vincent Pilaud (Universitat de Barcelona – Centre de Recerca Matemàtica) introduce the wiggly complex, a novel and rich combinatorial and geometric structure. Through a deep exploration of its properties (combinatorial, categorical, and geometric), they construct the wigglyhedron, a polytope that realizes this complex and connects it to broader mathematical frameworks such as Cambrian lattices, flip graphs, and representation theory.

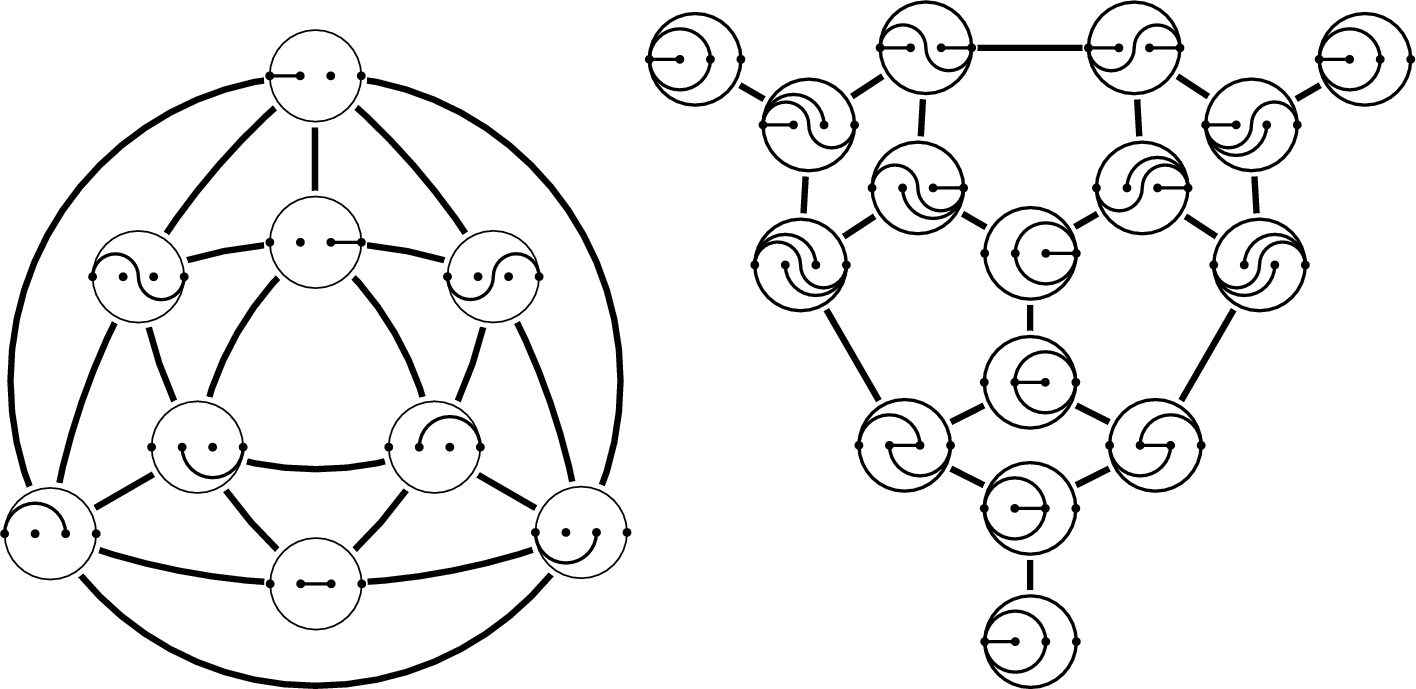
The wiggly complex (left) and the wiggly flip graph (right). Figure taken from the original publication.

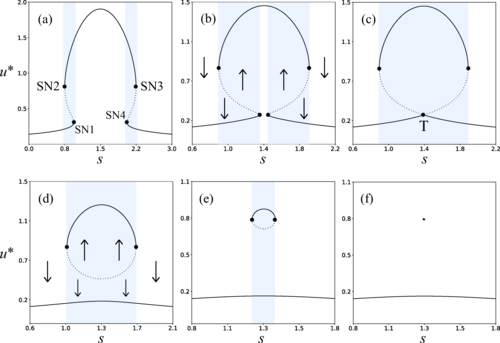
The journey begins with a simple idea: draw arcs between points on a line, allowing them to wiggle above and below the axis, but never cross. These wiggly arcs form the basis of the wiggly complex, a (2n−1)-dimensional pseudomanifold without boundary. It is the simplicial complex of pairwise pointed and non-crossing subsets of internal wiggly arcs.

The wiggly arcs were inspired by certain decompositions of arbitrary curvy paths between points arising from a geometric model in representation theory.
Given a set of points on along a line segment, they provide a combinatorial way to decide on which side of the line lies each point.
They also appeared in work of Nathan Reading on non-crossing arc diagrams, although the compatibility condition was very different.

— Vincent Pilaud (UB – CRM)

The vertices of the complex are the wiggly arcs themselves—curves that wiggle around n+2 collinear points. Its faces are sets of arcs that are pairwise pointed and non-crossing, and its facets—called wiggly pseudotriangulations—are maximal such sets. These pseudotriangulations divide the space into curved, triangle-like regions, forming the top-dimensional cells of the complex.

Four wiggly pseudotriangles. Figure taken from the original publication.

In my work, it is very important to experiment with the combinatorial objects, to get familiar with their properties and develop conjectures and statements. I do a lot of experiments using the open-source software sagemath. In particular, once we discovered the rule for the coordinates of the rays of the wiggly fan and of the facets of the wigglyhedron, it was interesting to look at the 3-dimensional wiggly fan and wigglyhedron that are represented in the paper.

— Vincent Pilaud (UB – CRM)

The wiggly complex is not just a geometric object—it encodes deep combinatorial structures. The authors define wiggly permutations, a class of pattern-avoiding permutations of [2n], and prove a bijection between these and wiggly pseudotriangulations. This bijection induces an isomorphism from the wiggly flip graph to the cover graph of the wiggly lattice. The wiggly permutations form a sublattice of the weak order on permutations (the wiggly lattice), whose Hasse diagram is regular of degree 2n−1 and isomorphic to the graph of the wigglyhedron oriented in a suitable direction.

The most surprising result is that the wiggly complex is the boundary complex of a polytope.
While simplicial complexes are very common in mathematics (they just encode collections of subsets closed under taking subsets), boundary complexes of polytopes are very specific.

— Vincent Pilaud (UB – CRM)

This lattice-theoretic viewpoint is enriched by a categorical one. Using the Khovanov–Seidel model, the authors interpret the decomposed objects in a triangulated category as wiggly arcs, whose intersections correspond to morphisms. Decomposing a general curve into wiggly arcs mirrors the decomposition of a complex object into its cohomology pieces.

Moreover, compatibility is defined both geometrically (non-crossing and pointedness) and categorically: each arc corresponds to an object in an abelian category, and compatibility reflects the absence of extensions between these objects. This dual interpretation allows the authors to connect geometry with homological algebra in a precise and elegant way.

Some incompatible wiggly arcs: non pointed (left) and crossing (right). Figure taken from the original publication

After developing the wiggly complex and its associated structures, the authors construct the wigglyhedron—a simplicial polytope whose polar has a boundary complex isomorphic to the wiggly complex. This polytope is defined in two equivalent ways:

• As the intersection of halfspaces defined by all internal wiggly arcs.
• As the convex hull of points associated with all wiggly pseudotriangulations.

The wigglyhedron has deep connections with representation theory (but I would not say that this was unexpected as the motivation for the definition came from that side).
Trying to extend the wigglyhedron to arbitrary point sets in the plane we also need to understand connections with rigidity theory (but this was also expected as this was already present in the work of Rote-Santos-Streinu).

— Vincent Pilaud (UB – CRM)

The collection of cones generated by the g-vectors of wiggly pseudodissections forms the wiggly fan, the normal fan of this simplicial polytope.

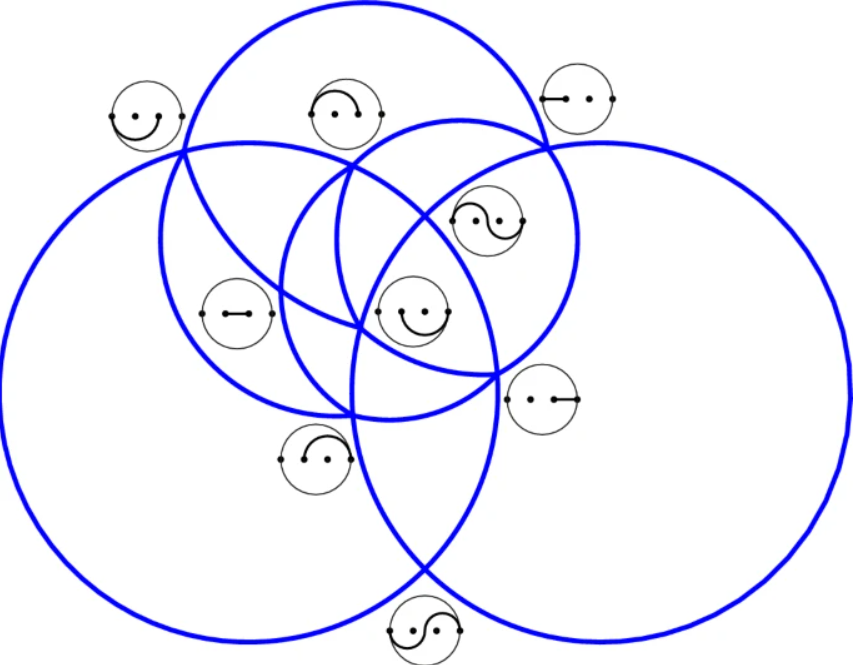
The wiggly fan WF2 , intersected with the unit sphere and projected stereographically to the plane. The vertices of the projection are rays of WF2 and are labeled by the corresponding wiggly arcs. Figure taken from the original publication

The wigglyhedron is not an isolated object. In fact, it embeds known structures from the Cambrian world:

• Any type A Cambrian associahedron is normally equivalent to a well-chosen face of the wigglyhedron.
• The corresponding Cambrian lattice—appearing through triangulations, permutations, wiggly pseudotriangulations, and wiggly permutations—emerges as an interval in the wiggly lattice.
• The Cambrian fan is a link in the wiggly fan.

These connections position the wigglyhedron as a unifying object in discrete geometry, capable of capturing and extending classical constructions.

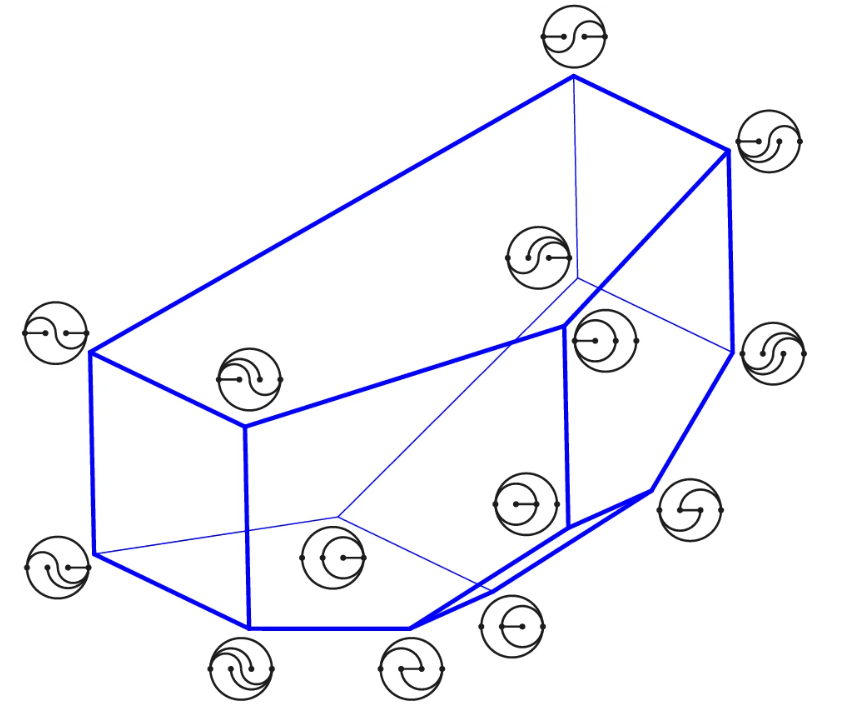
 The wigglyhedron W2 . The vertices are labeled by the corresponding wiggly pseudotriangulations. Figure taken from the original publication

The paper concludes with a rich set of open problems, grouped into three main areas:

Graphical and Geometric Properties

• What is the diameter of the wiggly flip graph?
• Does the wiggly complex satisfy the non-leaving face property, relevant to polytope navigation and optimization?
• Does the wiggly flip graph admit a Hamiltonian path or cycle?

Generalizations and Dualities

• Is there a dual interpretation of wiggly pseudotriangulations, as some sort of pseudoline arrangements?
• Can we define a multi-wiggly complex?
• Can the wiggly complex be extended to arbitrary finite Coxeter groups?

Categorical and Algebraic Questions

• Can we characterize maximal compatible collections of objects without reference to curves?
• Can such collections always be realized as cohomology pieces of a larger object?

I hope that our work will have consequences in representation theory. As I am not a representation theorist myself, it is difficult to imagine what it will bring there, but my experience indicates that it will certainly inspire future results.

— Vincent Pilaud (UB – CRM)

The wigglyhedron is not the starting point—it is the culmination of a deep exploration into the structure of the wiggly complex. Through a blend of geometry, combinatorics, and category theory, Bapat and Pilaud have introduced a new mathematical landscape, rich with connections and open questions. Their work lays the foundation for future discoveries at the intersection of discrete geometry and algebraic structures.

The most challenging open problem is to extend our study to the wiggly complex of arbitrary point sets in the plane. In our work, we consider the wiggly complex of a set of n aligned points and prove that it is the boundary complex of a polytope. Rote-Santos-Streinu had the same result for the pseudotriangulation complex (there is no wiggly here, the line segments are all straight) of a set of n points in general position in the plane (when no three points are aligned). These are the two extreme of a much more general situation of an arbitrary point set in the plane (not necessarily aligned, not necessarily in general position), for which there is a natural notion of wiggly complex which should be the boundary complex of a polytope as well.

— Vincent Pilaud (UB – CRM)