A recent article written by CRM PI Álvaro Corral (Complex Systems research group) has analysed the data from some of the largest known epidemics caused by infectious diseases, to prove that recent claims that the size distribution of such events is strongly fat-tailed may not be conclusive. According to the study, other distributions could explain the data just as well.
Being able to measure the final size reached by an epidemic is crucial to understand its impact. As we are currently in the midst of the COVID-19 pandemic, which has altered the world until almost bring it to a halt, we are still coping with the tremendous amount of data being collected worldwide regarding the number of deaths. Trying to prevent or even get ahead of the evolution of the pandemic has proved tricky for governments and experts. Using the right modelling tools could have important consequences for the management of the pandemic.
A paper published in May of last year by scientists Pasquale Cirillo and Nassim Taleb claimed that the fatality distribution in major epidemics through history, such as COVID-19, is ‘extremely fat-tailed’. Fat-tailed distributions decline more slowly, allowing for the emergence of outliers and extremes. We can see why this is relevant by looking at human height, for instance. Height is a value that is evenly distributed, which is why most people are less than two meters tall and we do not see three meters tall giants. However, with a fat-tailed distribution, the possibility for extreme occurrences becomes more probable, thus raising the risk of pandemics having a deeper impact on the population.
One of the limitations faced by scientists when studying the distribution of deaths caused by epidemic diseases is the incompleteness of the data available.
Such paradigms are of crucial importance in the study of complex systems, composed by many elements interacting with each other. Dr. Corral, principal investigator of the Complex Systems research group at the CRM, has recently studied the same data analysed by Cirillo and Taleb, in order to determine if other distribution models —not fat-tailed— could be also used to explain the tail of the distribution of fatalities during epidemics.
In his article, Corral uses a simulation of a truncated log-normal distribution, presenting a random variable with an evenly distributed logarithm, to successfully explain the data obtained from the epidemics studied. Consequently, we can assume that there is not enough empirical evidence to state that the deaths caused by pandemics follow a fat-tailed distribution. Thus, not only fat-tailed distributions could have enormous risks, but also other models of distribution could present very high risks as well. The article also presents an approximation of the projected final death toll from the current COVID-19 pandemic, though it acknowledges the limitations that such estimation has to overcome.
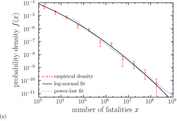
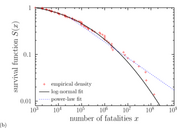
When studying the effects and magnitude of events such as the COVID-19 pandemic, it is crucial to contemplate different models, as well as using simulations to assess the soundness of the conclusions reached based on a limited amount of data. This could have a huge influence in how well prepared we are to face the next health crisis.