Critical Slowing Down in Genetic Systems: The Impact of Bifurcation Proximity and Noise

An international collaboration including researchers from the Centre de Recerca Matemàtica (CRM) has shown that when several bifurcations occur close to one another, their interaction can dramatically amplify critical slowing down effect – the progressive slowdown of trajectories near critical transitions. Published in Physical Review E, the study also shows that molecular noise can tune these transient times, offering new insights for synthetic biology and cellular decision-making.

When a dynamical system approaches a bifurcation, its trajectories slow down, meaning that small changes in conditions take longer to produce a response. This effect, known as critical slowing down, is well understood for isolated bifurcations. But what happens when several bifurcations occur close together? A new study published in Physical Review E shows that the interaction between nearby bifurcations can amplify this slowdown through nonlinear synergies. The work, titled “Local nearby bifurcations lead to synergies in critical slowing down: The case of mushroom bifurcations” was carried out by Mariona Fucho-Rius (Universitat Politècnica de Catalunya), Smitha Maretvadakethope and Rubén Pérez-Carrasco (Imperial College London), Àlex Haro (Universitat de Barcelona – Centre de Recerca Matemàtica), Tomás Alarcón (ICREA – Centre de Recerca Matemàtica), and Josep Sardanyés (Centre de Recerca Matemàtica). 

Background: Bifurcations and Complex Systems

In dynamical systems, a bifurcation marks a critical change in behavior as a control parameter varies, for instance, when a stable equilibrium disappears or new equilibria emerge. As the system approaches this point, its trajectories slow down before switching to a new regime, a phenomenon known as critical slowing down. It has been widely studied in cases where the transition is triggered by a single bifurcation.

However, in contexts like cellular biology, multiple nearby bifurcations often interact. This is especially relevant in genetic regulatory networks, where decision-making —such as cellular differentiation— depends not only on the final state of the system, but also on how long it takes to reach it.

Bifurcations and their associated scaling laws have been studied for decades and even tested experimentally in an electronic circuit in the work of Trickey and Virgin (Phys. Lett. A, 1998). However, the behavior of nearby bifurcations -how their proximity and mutual influence affect transient dynamics- remains largely unexplored. We were intrigued by this gap and wondered whether the combination of multiple local bifurcations could produce nonlinear, synergistic effects on critical slowing down. This question also connects directly with synthetic biology, where gene regulatory networks often operate close to several bifurcations: understanding their interplay could help us design genetic circuits or biosensors capable of fine-tuning their temporal responses.

— Mariona Fucho-Rius (UPC)

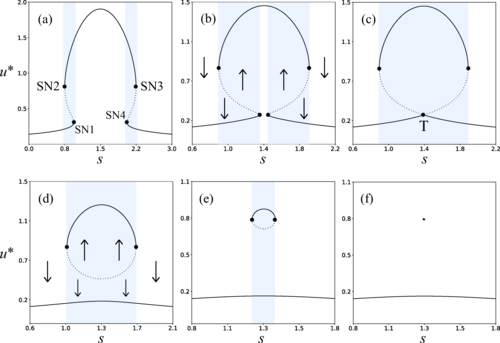
In this scenario, mushroom-shaped bifurcation diagrams —visual maps showing how a system’s behavior changes with varying conditions— offer a particularly interesting configuration. These diagrams arise in simple genetic models where a gene self-activates and is regulated by an external signal. Under certain conditions, four sudden change points (bifurcations) and three possible stable states appear, forming a structure reminiscent of a mushroom. Although these diagrams had been studied for their stationary behavior —such as bistability or memory— until now, their influence on the system’s temporal dynamics had not been analyzed.

Evolution of the mushroom bifurcation diagram.  Figure taken from the original publication.

This study starts precisely from that question: what happens to the transient times when two bifurcations are so close that they begin to interact?

We started by characterizing the types of bifurcations that appear in the so-called mushroom bifurcation diagram (four saddle-node bifurcations, two of which collide into a transcritical bifurcation). Once we analyzed the model mathematically, we confirmed analytically the coexistence of these bifurcations and could connect them to known scaling laws for each case. This analytical basis, supported by numerical simulations, revealed that the mushroom geometry provides an ideal setting to study what happens when several bifurcations coexist and interact, leading to synergistic critical slowing down effect.

— Mariona Fucho-Rius (UPC)

Findings: When Bifurcations Interact

The research team demonstrated —both analytically and numerically— that the proximity of bifurcations generates a synergistic effect on transition time: the system slows down much more than it would if each bifurcation acted independently. It’s not a sum of effects, but a nonlinear amplification of the slowdown.

They also studied how molecular noise —the fluctuations affecting the system— modulates this behavior. Intrinsic noise, caused by the random nature of biochemical reactions, can accelerate transitions but with less precision. Extrinsic noise, derived from environmental factors such as variability in cellular signals, tends to slow transitions but maintains low variability.

In our study, extrinsic noise slowed down transient times, in contrast with intrinsic noise, which tended to accelerate them. This means that by tuning the balance between these two noise sources, one could design systems that respond with a specific transient timing and a prescribed precision. In the context of synthetic biology, this could be exploited to engineer gene circuits or biosensors that display smooth and controllable transitions, effectively providing a way to modulate response sensitivity through noise. Moreover, this interplay between noise sources could enable the design of genetic clocks, which are systems where the duration of a transient acts as a controllable delay mechanism. Such timing control is fundamental in many biological contexts, from developmental decision-making to rhythmic gene expression.

— Mariona Fucho-Rius (UPC)

When both types of noise are introduced simultaneously, the average transition time and precision can be tuned, opening the door to adjustable genetic clocks. Moreover, the system can transition across a wider range of signals, thanks to a phenomenon known as noise-induced tipping, where random fluctuations push the system into a new stable state.

This discovery suggests molecular strategies for designing genetic circuits with transitions much slower than the typical timescales of the reactions involved. This is especially relevant in synthetic biology, where systems are built to respond with precision, flexibility, and temporal control.

We were surprised by how large the slowing-down effect became when the bifurcations were close. The combined impact of the two saddle-node bifurcations and the transcritical one was far greater than the sum of each taken separately. This synergistic amplification of transients (in a sense, “2 + 2 > 4”) was unexpected and suggested that nearby bifurcations can resonate with each other. That observation encouraged us to explore stochastic effects and also to consider other geometries, such as isolas -closed curves in the phase space-, where similar or even stronger temporal effects might emerge.

— Mariona Fucho-Rius (UPC)

What’s next: Open Questions and Future Directions

These results reveal a new mechanism for generating long, tunable transients using minimal genetic architectures, an approach that could be key for designing synthetic gene circuits with programmable timing and or graded responses instead of abrupt switches.

The results suggest promising research lines. On one hand, the design of genetic circuits that leverage bifurcation synergies to control transition timing. On the other, the study of how these effects apply to real systems, such as cellular transitions, biological memories, or molecular sensors.

It also opens the door to exploring the bifurcation landscape as a tool to design more robust and precise systems, and to use molecular noise not as interference, but as a control mechanism.

A natural next step would be to test these ideas experimentally, for instance by constructing a synthetic gene circuit in bacteria that reproduces the mushroom-like bifurcation structure. Such experiments would allow us to measure the predicted transient extensions and study how intrinsic and extrinsic noise shape timing in living systems. Another exciting line of study is to study how other geometries, such as isola formations or higher-dimensional analogues, affect stochastic dynamics. 

— Mariona Fucho-Rius (UPC)

Additionally, the authors point to future directions such as:

• Studying overshooting in nearby bifurcations —a temporary overshoot of the system beyond its target state—, which could reduce the likelihood of abrupt transitions.
• Analyzing multidimensional systems, with multiple genes and interconnected bifurcations.
• Exploring new dynamic regimes in genetic regulatory networks (GRNs), with applications in synthetic biology, personalized medicine, and molecular engineering.
• Overall, this research opens a new perspective on time control in biological systems, with the potential to transform how we understand and design cellular decision-making processes.