The researchers Maicol Caponi, Alessandro Carbotti, and Alberto Maione extended the H- and Γ-convergence theories to the setting of nonlocal linear operators and their corresponding energies. The authors were able to overcome the limitations of classical localization techniques. If symmetry is also assumed, their results preserve key equivalences between the convergences. The work has been published in Calculus of Variations and Partial Differential Equations.
“The IP4RG program was crucial. It gave us the chance to spend two intense weeks working side by side on the project, which really accelerated our progress. Just as important were the informal discussions with other participants—those conversations often led to fresh insights and even helped us solve lingering issues, such as the uniqueness of the H-limit.”
— Maicol Caponi (Università degli Studi dell’Aquila), Alessandro Carbotti (Università del Salento) and Alberto Maione (Centre de Recerca Matemàtica)
The researchers Maicol Caponi (Università degli Studi dell’Aquila), Alessandro Carbotti (Università del Salento), and Alberto Maione (Centre de Recerca Matemàtica) have extended the classical theories of H- and Γ-convergence to a nonlocal setting—an investigation supported by the Centre de Recerca Matemàtica of Barcelona (CRM), under the International Programme for Research in Groups (IP4RG). Their work focuses on linear operators in fractional divergence form. To tackle the analytical challenges, they introduce new ideas that bypass the failure of traditional localization techniques in this (nonlocal) context. After proving the H-compactness for such a class of operators, involving general (possibly non-symmetric) matrices, in the second part of the work they focus on the symmetric case. They obtain in this scenario the equivalence between H-convergence of the operators and Γ-convergence of the corresponding nonlocal energies. As a consequence, they provide an alternative (variational) proof of the H-compactness theorem through Γ-convergence. The article has been published in Calculus of Variations and Partial Differential Equations.
Understanding H- and Γ-convergence: A Glimpse into the Mathematical Approximation
Imagine trying to understand the behavior of a complex material—say, a sponge with tiny holes—without knowing every detail of its internal structure. Instead of describing each part, you look for a simpler model that captures its overall behavior. This is the essence of the mathematical theory of homogenization, which emerged in the 1970s, driven by the need to understand how complex materials—like composites (structures made by layering sheets of different substances) or homogeneous materials with holes filled by another material —respond to external forces. It was done without modeling every microscopic detail, but with equations that capture the macroscopic behavior.
Mathematically, these systems are represented by partial differential equations with rapidly oscillating coefficients, such as:
where the matrix A(x) encodes the material properties at each point —acting like a parameter that varies across different materials.
To understand how solutions behave when these coefficients oscillate rapidly, researchers developed key notions of convergence:
- G-convergence was the starting point. Introduced by Spagnolo in the 1970s, it studies how sequences of differential operators behave in the limit. It’s useful for modeling materials with varying properties, but it has limitations—especially when dealing with non-symmetric matrices, which appear in many real-world applications.
- H-convergence was developed by Tartar and Murat to overcome the limitations of G-convergence. It refines the theory for non-symmetric cases, ensuring the uniqueness of the representation limit operator even when the matrices are not symmetric. In other words, it provides a robust framework for studying how sequences of differential operators behave in heterogeneous or irregular media.
- Γ-convergence takes a complementary (indirect) approach. Instead of focusing on operators, it deals with energy functionals—mathematical expressions that quantify the “cost” or “effort” of a system’s configuration. Γ-convergence ensures that the minimizers (optimal configurations) of approximating problems converge to the minimizer of the limit problem.
These concepts are not just abstract tools—they underpin models in electrostatics, magnetostatics, heat transfer, and elasticity, where might represent potential, temperature, or displacement, and encodes physical properties like conductivity or elasticity. Building on this foundational understanding, the researchers present a significant extension of these classical tools to a nonlocal setting.
“A very helpful idea, which goes back to a paper by C. Kreisbeck and H. Schönberger, is that fractional gradient and divergence can be expressed in terms of the classical (local) ones, applied to suitably transformed functions. This creates a bridge between the fractional and the local frameworks, allowing us to pass from one setting to the other.”
— Maicol Caponi (Università degli Studi dell’Aquila), Alessandro Carbotti (Università del Salento) and Alberto Maione (Centre de Recerca Matemàtica)
Returning to the sponge analogy
G-convergence tells you how the equations describing the sponge change as its internal structure varies.
H-convergence ensures that even if the internal forces are asymmetric, the model still behaves predictably.
Γ-convergence focuses on the energy needed to deform the sponge, ensuring that the most efficient way to press it remains consistent as the structure changes.
What’s New? Key Innovations in Nonlocal Theory
Caponi, Carbotti and Maione present a significant extension of classical mathematical tools—H-convergence and Γ-convergence—to a nonlocal setting, which is increasingly relevant in modern applications such as fluid mechanics, image processing or anomalous diffusion. This shift is significant because traditional localization techniques fail in nonlocal contexts, where interactions are not confined to infinitesimal neighborhoods.
“The initial motivation came from a paper by a group of researchers (Fernández Bonder, J.; Ritorto, A.; Salort, A.M.) who had been exploring related ideas in a different framework. A key turning point came during a meeting in August in Perugia (Italy), when we suddenly realized that the question of uniqueness in the nonlocal setting was far from being trivial.”
— Maicol Caponi (Università degli Studi dell’Aquila), Alessandro Carbotti (Università del Salento) and Alberto Maione (Centre de Recerca Matemàtica)
In particular, they study the H-convergence of nonlocal linear operators in fractional divergence form, where the oscillations of the matrices are prescribed outside the reference domain. This setup reflects realistic scenarios in which the material properties vary globally, not just locally, and introduces significant analytical challenges.
The first central result of the paper is the H-compactness of a class on linear nonlocal operators. The authors overcome the limitations of traditional (local) techniques, by taking advantatge of the classical (local) theory to prove the existence of a H-limit in the nonlocal scenario. They build the limit operator as a reasonable extention of the local one, and finally show that this is the only possible (unique) representation of the limit. This is crucial for studying heterogeneous materials with complex internal structures.
“Actually, we don’t introduce a new compactness argument. What we do prove is a consistency result between the local and the nonlocal settings. In simple terms, we show that if a local H-limit exists, then there’s a corresponding nonlocal H-limit described by the same operator. So, by relying on the well-known compactness of local H-convergence, we automatically obtain compactness in the nonlocal case as well.”
— Maicol Caponi (Università degli Studi dell’Aquila), Alessandro Carbotti (Università del Salento) and Alberto Maione (Centre de Recerca Matemàtica)
A key innovation is the use of fractional gradient and divergence operators, which allow researchers to define a nonlocal H-convergence using differential operators — even in the presence of matrix-valued coefficients, essential for modeling anisotropic heterogeneous materials (direction-dependent materials).
The second central result of the paper is that, under symmetry assumptions, the classical equivalence between H-convergence (which describes how differential operators behave) and Γ-convergence (which describes how energies behave) still holds in this nonlocal framework. This means that the mathematical structure remains consistent even when moving from local to nonlocal models.
“Unlike the local case, fractional operators do not allow for standard localization techniques. This makes many classical arguments no longer applicable. One of the hardest parts was proving the uniqueness of the H-limit and of the integral representation of the Γ-limit. Without the latter, the connection between H-convergence and Γ-convergence would have remained incomplete. The uniqueness was proved in our second meeting in person that happened at CRM last March, almost six months after the first preprint version of our paper.”
— Maicol Caponi (Università degli Studi dell’Aquila), Alessandro Carbotti (Università del Salento) and Alberto Maione (Centre de Recerca Matemàtica)
In short, the article provides new tools to study complex systems where long-range interactions matter, and it opens the door to applying these ideas in fields like physics, engineering, and data science.
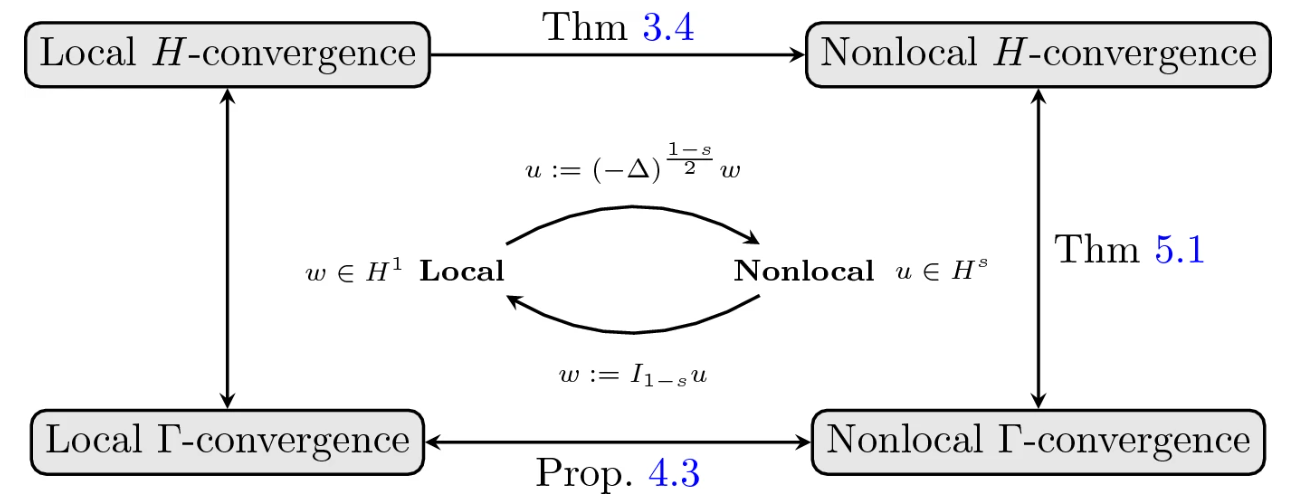
The diagram illustrates the current state of the art and the main contribution of the article. While the first vertical arrow on the left was already known in the literature since the 1980s, all other arrows completing the square represent new results established in this work. Figure taken from the original publication.
What’s Next? Open Challenges and Promising Paths in Nonlocal Analysis
“In the local setting, it is known that, under a suitable construction of associated energies, the equivalence between H-convergence and Γ-convergence still holds even without symmetry. We believe that this construction could be adapted to the nonlocal case, although the local proofs are already quite technical, so extending it will not be easy.”
— Maicol Caponi (Università degli Studi dell’Aquila), Alessandro Carbotti (Università del Salento) and Alberto Maione (Centre de Recerca Matemàtica)
This work opens several avenues for further research:
Theoretical Challenges
- Beyond symmetry: The equivalence between H- and Γ-convergence is proven under symmetry assumptions. Extending this result to non-symmetric matrices remains an open and challenging question, especially in the fractional nonlocal setting where no natural energy is associated a priori.
- Extension to nonlinear operators: The current results focus on quadratic energies. In a forthcoming paper the authors and collaborators (Giuseppe Cosma Brusca and Fabio Paronetto) will address the nonlinear case of monotone operators with p-growth, aiming to generalize classical results to the fractional nonlinear nonlocal setting. This new research started during the IP4RG programme hosted at CRM last March.
Connections to Other Mathematical Frameworks
- Dirichlet forms and probabilistic interpretations: The connection with Dirichlet forms is not fully understood in the fractional setting. Exploring whether fractional quadratic forms define Dirichlet structures could link this theory to stochastic processes.
- Sub-Riemannian geometries: The notion of H-convergence has recently been extended to sub-Riemannian structures. Investigating compactness properties of fractional-order operators in settings such as Carnot groups could provide a structured framework for nonlocal analysis in geometric contexts.
- Alternative frameworks: compare the notion of nonlocal H-convergence introduced in this work with alternative definitions based on functional analytic approaches.
Applications and Computational Aspects
- Parabolic nonlocal operators: Once H-convergence is fully understood for elliptic operators, it is natural to study the asymptotic behavior of sequences of parabolic nonlocal operators. Preliminary results suggest that, in case of time-independent coefficients, the parabolic H-limit coincides with the elliptic one. Extending this to the nonlocal case is a promising direction.
- Applications in data science and imaging: Nonlocal models are increasingly used in image processing and machine learning. Exploring whether these convergence theories can offer new insights or guarantees in these fields remains an exciting possibility.
These open questions highlight the richness of nonlocal analysis and its potential to unify diverse mathematical frameworks.
This article lays the foundation for a unified theory of convergences in nonlocal models, bridging operator and variational perspectives, and opening the door to applications across mathematics, physics, and engineering.
“Two directions excite us the most. One is extending these results to nonlinear nonlocal operators, which would open up many new questions. The other is bringing the theory to non-Euclidean spaces.”
— Maicol Caponi (Università degli Studi dell’Aquila), Alessandro Carbotti (Università del Salento) and Alberto Maione (Centre de Recerca Matemàtica)
|
|
CRM CommNatalia Vallina
|
CRM Awards Its Prize at Exporecerca Jove for the Third Time
For the third year running, CRM visited Exporecerca Jove to award its prize to the student project with the strongest mathematical content. This edition, the jury selected two winners: Xavier Ortiz Quintana, who built a real-time 3D scanner using...
When Symmetry Breaks the Rules: From Askey–Wilson Polynomials to Functions
Researchers Tom Koornwinder (U. Amsterdam) and Marta Mazzocco (ICREA-UPC-CRM) published a paper in Indagationes Mathematicae exploring DAHA symmetries. Their work shows that these symmetries shift Askey–Wilson polynomials into a continuous functional setting,and...
Homotopy Theory Conference Brings Together Diverse Research Perspectives
The Centre de Recerca Matemàtica hosted 75 mathematicians from over 20 countries for the Homotopy Structures in Barcelona conference, held February 9-13, 2026. Fourteen invited speakers presented research spanning rational equivariant cohomology theories, isovariant...
Three ICM speakers headline the first CRM Faculty Colloquium
On 19 February 2026, the Centre de Recerca Matemàtica inaugurated its first CRM Faculty Colloquium, a new quarterly event designed to bring together the mathematical community around the research carried out by scientists affiliated with the Centre. The CRM auditorium...
Trivial matemàtiques 11F-2026
Rescuing Data from the Pandemic: A Method to Correct Healthcare Shocks
When COVID-19 lockdowns disrupted healthcare in 2020, insurance companies discarded their data; claims had dropped 15%, and patterns made no sense. A new paper in Insurance: Mathematics and Economics shows how to rescue that information by...
L’exposició “Figures Visibles” s’inaugura a la FME-UPC
L'exposició "Figures Visibles", produïda pel CRM, s'ha inaugurat avui al vestíbul de la Facultat de Matemàtiques i Estadística (FME) de la UPC coincidint amb el Dia Internacional de la Nena i la Dona en la Ciència. La mostra recull la trajectòria...
Xavier Tolsa rep el Premi Ciutat de Barcelona per un resultat clau en matemàtica fonamental
L’investigador Xavier Tolsa (ICREA–UAB–CRM) ha estat guardonat amb el Premi Ciutat de Barcelona 2025 en la categoria de Ciències Fonamentals i Matemàtiques, un reconeixement que atorga l’Ajuntament de Barcelona i que enguany arriba a la seva 76a edició. L’acte de...
Axel Masó Returns to CRM as a Postdoctoral Researcher
Axel Masó returns to CRM as a postdoctoral researcher after a two-year stint at the Knowledge Transfer Unit. He joins the Mathematical Biology research group and KTU to work on the Neuromunt project, an interdisciplinary initiative that studies...
The 4th Barcelona Weekend on Operator Algebras: Open Problems, New Results, and Community
The 4th Barcelona Weekend on Operator Algebras, held at the CRM on January 30–31, 2026, brought together experts to discuss recent advances and open problems in the field.The event strengthened the exchange of ideas within the community and reinforced the CRM’s role...
From Phase Separation to Chromosome Architecture: Ander Movilla Joins CRM as Beatriu de Pinós Fellow
Ander Movilla has joined CRM as a Beatriu de Pinós postdoctoral fellow. Working with Tomás Alarcón, Movilla will develop mathematical models that capture not just the static architecture of DNA but its dynamic behaviour; how chromosome contacts shift as chemical marks...
Criteris de priorització de les sol·licituds dels ajuts Joan Oró per a la contractació de personal investigador predoctoral en formació (FI) 2026
A continuació podeu consultar la publicació dels criteris de priorització de les sol·licituds dels ajuts Joan Oró per a la contractació de personal investigador predoctoral en formació (FI 2026), dirigits a les universitats públiques i privades del...















