An Introduction to Equilibrium Problems and their applications
An Introduction to Equilibrium Problems and their applications
(10 hours)
Registering required.
UPF Campus Ciutadella, C/ Trias-Fargas, 25, Barcelona.
The term equilibrium has been widely used in mathematics, physics, chemistry, biology, engineering and economics within different frameworks. Many equilibrium problems can be formulated through different mathematical models such as complementarity, variational inequalities, multiobjective optimization, noncooperative games and inverse optimization among others.
All these mathematical models share an underlying common structure that allows to formulate them in a unique format: the so-called Ky Fan inequality. The goal of this course is to provide a comprehensive overview of the main theoretical results and solution algorithms for Ky Fan inequalities, together with a wealth of applications. Particular emphasis is given to the role of nonlinear optimization techniques as valuable tools for analyzing and solving Ky Fan inequalities.
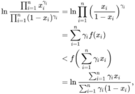
(10 hours)
Registering required.
UPF Campus Ciutadella, C/ Trias-Fargas, 25, Barcelona.
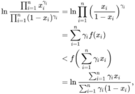
The term equilibrium has been widely used in mathematics, physics, chemistry, biology, engineering and economics within different frameworks. Many equilibrium problems can be formulated through different mathematical models such as complementarity, variational inequalities, multiobjective optimization, noncooperative games and inverse optimization among others.
All these mathematical models share an underlying common structure that allows to formulate them in a unique format: the so-called Ky Fan inequality. The goal of this course is to provide a comprehensive overview of the main theoretical results and solution algorithms for Ky Fan inequalities, together with a wealth of applications. Particular emphasis is given to the role of nonlinear optimization techniques as valuable tools for analyzing and solving Ky Fan inequalities.

Mauro Passacantando, University of Pisa
Biosketch
Mauro Passacantando received both M.Sc. and Ph.D. in Mathematics from the University of Pisa. He is currently Assistant Professor of Operations Research at the Department of Computer Science of the same university. He achieved the Italian National Habilitation for full professorship in Operations Research. His research activities are mainly focused on variational inequalities, projected dynamical systems, equilibrium problems, and their applications. Most of his recent work focuses on theory and algorithms for Ky Fan inequalities and on game theoretic approaches to service provisioning problems in cloud and multi-cloud systems. He is author of one monograph and more than forty scientific papers published in international journals and volumes.
Contents
- Equilibrium models and applications: complementarity (obstacle problem), variational inequalities (traffic networks), noncooperative games (power control in wireless communications), multiobjective optimization (portfolio selection), fixed point (input-output analysis in an economy), saddle point (optimal production under restricted resources), inverse optimization (quality control in production systems). Ky Fan inequalities: a unifying equilibrium model.
- Convexity and monotonicity tools, equivalent reformulations, existence of equilibria.
- Uniqueness of equilibria, stability and well-posedness, error bounds.
- Fixed-point methods, extragradient methods with and without line search.
- Descent methods based on gap and D-gap functions, regularization methods, proximal point methods, computational issues.
References
- Bigi G., Castellani M., Pappalardo M., Passacantando M., Nonlinear Programming Techniques for Equilibria, Springer, 2019.
- Bigi G., Castellani M., Pappalardo M., Passacantando M., Existence and solution methods for equilibria, European Journal of Operational Research, vol. 227 (1), pp. 1-11, 2013.
- Facchinei F., Pang, J.-S., Finite-dimensional variational inequalities and complementarity problems, Springer, 2003.
- Konnov I.V., Equilibrium models and variational inequalities, Elsevier, 2007.
